This two-part genetics series will introduce the fundamentals of heredity and genetics and how a dog’s genetic code determines its outward appearance. We’ll cover some basic principles and terminology in the first part, and go over probability of inheritance and litter statistics in the second part.
Need to review the basics? Click here to go back to part one.
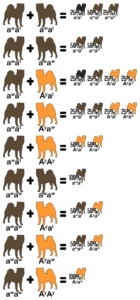
It has come to my attention that some disreputable sources are referencing these articles, so be aware that brown (aka liver or chocolate), dilute (aka blue), lilac (aka isabella), merle, and any other colors or patterns not specifically mentioned in this article are not native to the Japanese breeds and is the direct result of mixing with other breeds. In addition, except for merle, these colors can only occur if both parents are mixed.
Genotypes and Phenotypes
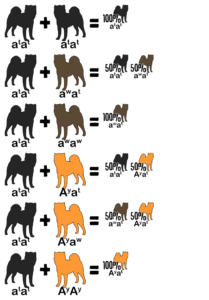
Reference the following table to determine the genotype from a dog’s appearance and vice versa. A dash indicates an unknown allele masked by a dominant allele or epistatic gene. For example, E- is a placeholder for EE or Ee; the dog is colored but might be a carrier for white. The K Locus and A Locus genes cannot be determined by looking at a white dog; anything is possible underneath the white.
| Color | E Locus | K Locus | A Locus |
|---|---|---|---|
| Red | E- | kyky | Ay– |
| Sesame | E- | kyky | aw– |
| Black and Tan | E- | kyky | atat |
| ✦ Brindle Point | E- | kbr– | atat |
| Brindle | E- | kbr– | Ay– |
| ✦ Sesame Brindle | E- | kbr– | aw– |
| White | ee | – – | – – |
If a dog has two copies of the same allele, for example EE or ee, it is homozygous for that trait. Homozygous dogs are true-breeding, which means they always pass down the same allele to their offspring. When a dog’s parents are true-breeding, it is possible to determine what hidden alleles it carries. For example, a brindle dog is E- kbr– Ay– per the chart above. If the dog has a white father (ee) and black and tan mother (E- kyky atat), it must inherit e from the father and ky at from the mother, making its complete genotype Ee kbrky Ayat.
If the dog has one copy of two different alleles, for example Ee, it is heterozygous. These dogs are hybrids and have an equal chance to pass down either allele to their offspring. When a dog’s offspring express a recessive phenotype that differs from its own, the dog must be a hybrid. For example, a sesame dog is E- per the chart above. If the dog has a white daughter (ee), it must have donated an e allele to her, making its genotype Ee.
Be careful; offspring with a recessive trait confirm that both parents are carriers, but the absence of such offspring does not confirm that the parents are not carriers.
Probability of Inheritance
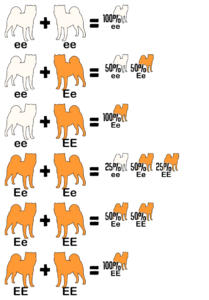
The value of studying coat color genetics is in being able to predict the likelihood of inheriting particular colors. A Punnett square is a mathematical visual aid used to predict the chances of an offspring to have its parents’ traits. These squares are most commonly divided into four parts, with each part equaling a 25% chance of the offspring receiving that set of genes. One parent’s alleles are written across the top and the other parent’s alleles are written down the left side.
Example #1
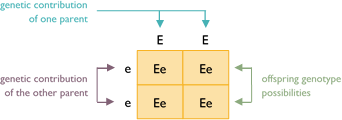
This Punnett square shows the result of crossing two true-breeding parents. One parent is colored (EE) and the other is white (ee). All offspring receive the same alleles from each parent. Each puppy is a colored hybrid that carries white (Ee).
Example #2
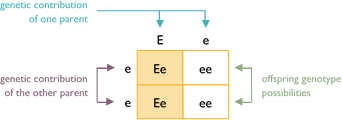
This is a cross between a white (ee) dog and a colored dog carrying white (Ee). The true-breeding white parent donates an e allele to all the offspring. However, the hybrid parent can give E or e. Each puppy has a 50% chance to be colored carrying white (Ee) or 50% chance to be white (ee).
Example #3
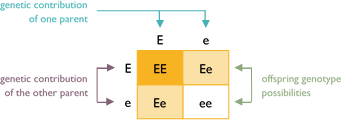
In this example, both parents are colored hybrids carrying white (Ee). The offspring can receive either an E or e allele from each parent. Each puppy has a 75% chance to be colored (EE or Ee) or 25% chance to be white (ee). Of the colored puppies, each has a 67% chance to carry white (Ee).
Calculating Complex Crosses
The Punnett square is a valuable tool, but not ideal for calculating probabilities of inheritance of multiple genes. Each additional gene increases the number of combinations by a factor of four; to chart all three coat color genes affecting the Japanese breeds, it would require 64 squares and be quite clunky and prone to human error. Fortunately, this is just a visual way of representing probability calculations, which can be done without the Punnett square and still arrive at the same result.
The alleles that one parent donates to its offspring do not influence the alleles that the other parent donates; each of these events are independent of one another. The probability or two or more independent events occurring together can be calculated by multiplying the individual probabilities of the events. For instance, consider the cross between two Ee dogs above. Each parent has a 50% chance of donating an e allele to a puppy, so the probability of getting a white (ee) puppy is 50% × 50% = 25%.
In this same example, there are three different genotypes which result in a colored puppy:
- Receives E from father and E from mother (50% × 50% = 25% chance)
- Receives E from father and e from mother (50% × 50% = 25% chance)
- Receives e from father and E from mother (50% × 50% = 25% chance)
These events cannot happen at the same time, since a puppy only receives one copy of each gene from each parent. To calculate the probability that any one of mutually exclusive events occurs, add the individual probabilities of the events together. In this case, 25% + 25% + 25% = 75% total chance of a colored puppy (EE or Ee).
Although a puppy has a 75% chance to have the colored phenotype, some of the colored puppies may be carriers for white. To find the probability that an individual with dominant phenotype carries a hidden recessive, divide the genotype probability by the phenotype probability. Using the rule of mutually exclusive events, there is a 50% chance of a colored puppy carrying white (Ee). Therefor there is a 50% ÷ 75% = 67% chance that a colored puppy from this cross carries white.
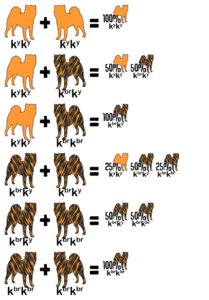
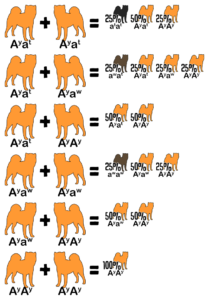
Example #4

The Punnett squares above represent a cross between two Japanese Akita. In this breed, ky non-brindle is always red. One parent is white masking brindle and red (ee kbrky) and the other is brindle carrying white and red (Ee kbrky). Each puppy has an equal chance to be colored (Ee) or white (ee). They each have an independent 75% chance to be brindle (kbrkbr or kbrky) or 25% chance to be red (kyky). Lastly, they each have a 50/50 chance to be male or female. These are all independent probabilities. To calculate the odds that a puppy is colored, red, and female multiply the individual probabilities together: 50% × 25% × 50% = 6.25%.
Pre-calculated probabilities for all coat colors of the Japanese breeds appear at the end of this document.
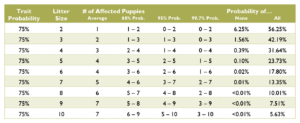
Litter Statistics
Each puppy’s genotype is independent of every other puppy in the litter. In other words, the sex, color, and other traits of one puppy has nothing to do with the traits of its siblings. If the first four puppies are female, the fifth puppy still has a 50% chance to be male or female; it is not “due” to be male simply because the high number of females departs from the expected average. The Gambler’s Fallacy is based on a failure to understand statistical independence, or a belief that a past independent trial will affect a future independent trial.
Over time, with a sample size of hundreds or even thousands of puppies, the ratios of genotypes will resemble the percent probabilities. However, with the small sample size of a litter, it is not unusual for the ratios to be wildly different from predicted. It is incorrect to say that there will be, should be, or usually is a certain percent of the litter matching a given genotype or phenotype. For example, just because an individual puppy has a 25% chance to be white does not mean that 25% of the puppies will be white. Never apply individual probabilities to the litter as a whole.
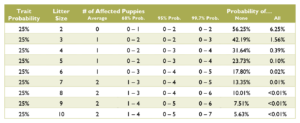
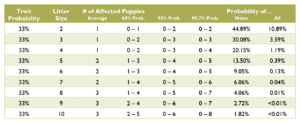
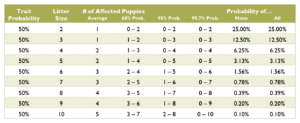
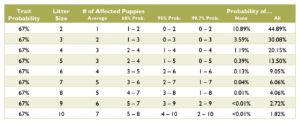
Calculating the probabilities for a litter is quite a bit more complex than those for an individual puppy, and requires multiple chapters on statistics covering samples and populations, sample size, significance, binomial probability, mean and variance, standard deviation, confidence interval, normal distribution, the law of averages, hypothesis testing, and a long list of fallacies. Such in depth explanation greatly exceeds the scope of this document. Instead, see the charts below for common probabilities and statistics about affected puppies by litter size.
Coat Color Probabilities for Japanese Breeds
The percentages are a probability for each puppy not a percentage of the litter.